PowerExpect

Posté le 13 octobre 2025 • 28 min de lecture • 5 940 mots

Marchés De L'électricité Prévision De Séries Temporelles Machine Learning/Deep Learning

Partager via

Lien copié dans le presse-papier

Une app rapide et simple permettant de consulter les prix prévisionnels et réels de l'électricité pour les zones d'enchères FR et DE/LU.

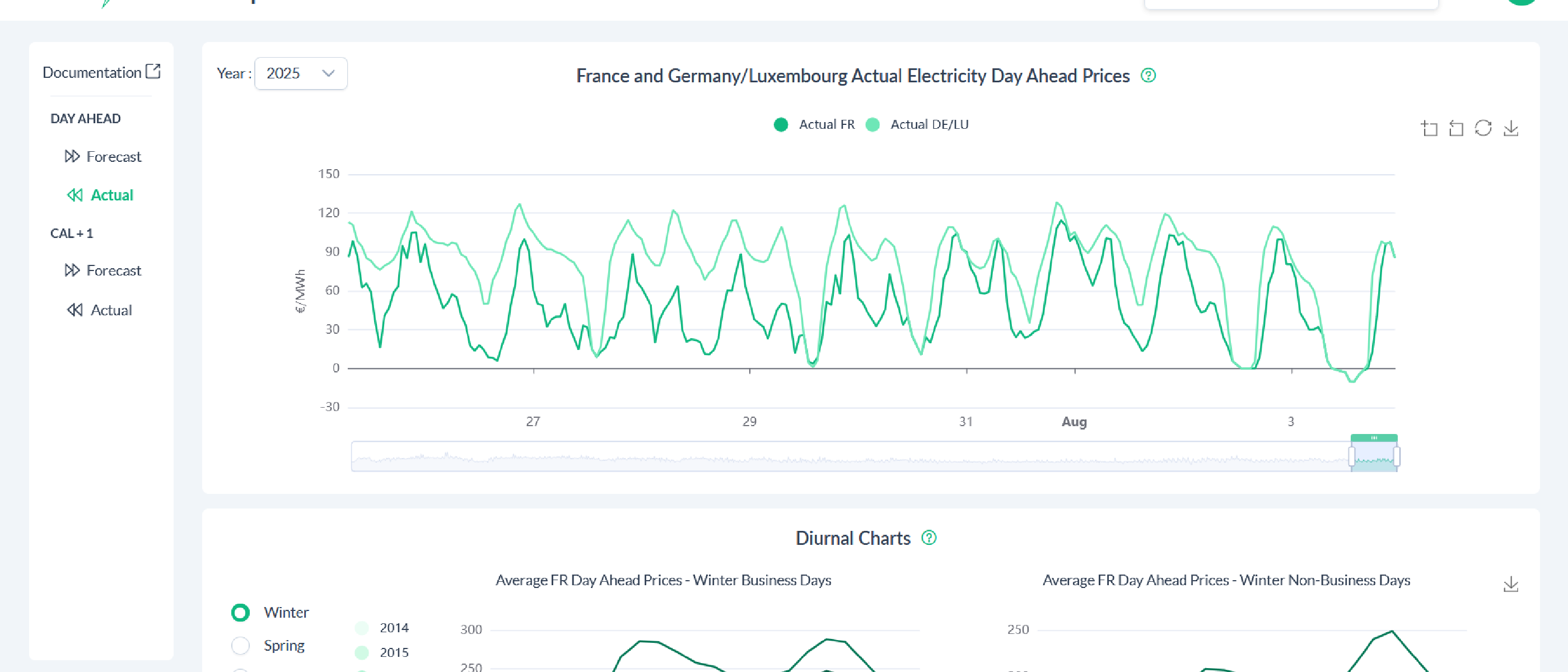
Ouvrir l’app

Cliquez ici

1. Motivation

L’objectif initial de ce projet était double: D’une part apprendre un framework spécialisé dans le frontend, et d’autre part tester de nouvelles méthodes/architectures de prévisions de séries temporelles appliquées à la prévision du prix de l’électricité.

En effet, les librairies python de frontend sont souvent limitées et/ou lentes. Je voulais donc tester un framework spécialisé dans le développement frontend d’applications web. Mon choix s’est porté sur Vue.js qui semblait être le plus accessible rapidement.

Je souhaitais également disposer d’un outil complet avec lequel je pouvais facilement tester en conditions réelles de nouvelles méthodes et de nouveaux modèles de prévision de séries temporelles et notamment de prévision des prix de l’électricité. Lorsque l’on travaille dans l’industrie sur ce type de projet, on préfère généralement utiliser ce que l’on sait qui marche déjà bien en suivant le rasoir d’Occam et sous la contrainte du temps. Il y a donc souvent peu de place à l’exploration profonde de nouvelles choses. Or la littérature est très prolifique sur le sujet d’où ma curiosité.

2. Introduction

La prévision des prix de l’électricité (EPF/“Electricity Price Forecasting”) est un domaine d’application de méthodes de prévision de séries temporelles (TSF/“Time Series Forecasting”) bien connu. Ce problème est exploré depuis maintenant plus de 30 ans après le début de la vague de libéralisation des marchés de l’électricité dans les années 90 et rencontre un intérêt de plus en plus grand dans la littérature [1]. C’est tout d’abord parce que la prévision de séries temporelles connaît elle même un interêt croissant [2] et ensuite parce que l’EPF joue un rôle fondamental sur les marchés de l’énergie, permettant aux acteurs du marché d’optimiser leurs stratégies de trading, de diminuer les risques financiers et de maintenir la stabilité du réseau. Cependant, l’exercice est complexe (et de plus en plus) car les fluctuations de prix à court terme sont très sensibles aux prévisions de production d’énergie renouvelable, aux annonces réglementaires et géopolitiques, et aux perturbations imprévues telles que les pannes de production ou les contraintes de réseau. Il en résulte des prix avec une forte volatilité, non-linéarité et des pics soudains [3]. Il existe plusieurs méthodes d’EPF, seules celles qui concernent l’apprentissage automatique (ML) nous intéressent ici.

L’histoire de l’EPF a donc suivie de près celle du TSF. Cette dernière a commencé avec des méthodes statistiques à base de moyennes mobiles développées dans les années 50 à 70 (Lissage exponentiel / ARIMA). Elle a ensuite continuée avec les premières méthodes de ML comme les arbres de décision dans les années 80 puis les GBM (Gradient Boosting Machines) en 1999/2001. En parallèle, des modèles d’apprentissage profond (DL) ont fait leur apparition avec les RNN et les LSTM dans les années 90 [2].

Ces briques fondamentales ont par la suite été étendues, améliorées et combinées pour fabriquer la myriade d’architectures que l’on connaît aujourd’hui. Des implémentations populaires de GBM comme XGBoost ou LightGBM, qui par ailleurs n’ont pas été conçues spécifiquement pour la prévision de séries temporelles, sont apparues dans les années 2010 et sont très vite devenues des références dans le domaine grâce à leur performance et leur interprétabilité. Les modèles de Deep Learning ont reçu une attention croissante avec par exemple des architectures à base de MLP (Perceptron Multi-Couche/Multi Layer Perceptron) comme NBEATS ou TIDE ou encore à base de transformeurs comme PatchTST ou PETformer. Dans le sillage de l’essor des modèles de fondation pour le traitement du langage naturel, des modèles de fondation pour la prévision des séries temporelles ont fait leur apparition tels que TimeGPT ou Lag-Llama. On a également pu voir des avancées dans d’autres architectures comme les modèles Mamba ou sur des aspects connexes comme le feature engineering. Dans l’ensemble, la prévision de séries temporelles constitue un domaine de recherche particulièrement dynamique et fécond, où de nombreuses pistes semblent avoir du potentiel [2].

L’objectif de l’EPF (et plus généralement du TSF) est de trouver une approximation satisfaisante selon certaines métriques de la fonction:

f : Z = \Big(\pmb{y}_{t-L+1:t},\;\pmb{X}^{(n)}_{t-L+1:t},\;\pmb{X}^{(m)}_{t+1:t+H}\Big) \longmapsto f(Z) = \pmb{\hat{y}}_{t+1:t+H}

Avec:

$L$ = La taille de la fenêtre des observations passées
$H$ = L’horizon de prévision
$n$ = Le nombre de variables explicatives
$m$ = Le nombre de variables explicatives disponibles sur l’horizon de prévision ( $m \le n$ )
$\pmb{y}_{t-L+1:t} \in \mathbb{R}^{\,L}$ = Le vecteur colonne des $L$ observations passées de la variable cible
$\pmb{X}^{(n)}_{t-L+1:t} \in \mathbb{R}^{\,L \times n}$ = La matrice des $n$ variables explicatives sur $L$ pas de temps
$\pmb{X}^{(m)}_{t+1:t+H} \in \mathbb{R}^{\,H \times m}$ = La matrice des $m$ variables explicatives sur l’horizon $H$
$\pmb{\hat{y}}_{t+1:t+H} \in \mathbb{R}^{\,H}$ = Le vecteur de la prévision de la variable cible sur l’horizon $H$

Le choix de $f$ est un choix d’architecture. Il repose sur plusieurs aspects comme notre connaissance du domaine d’application, notre conviction sur la capacité de l’architecture à modéliser les relations entre les variables explicatives et la variable cible pour ce problème ou encore notre compréhension de la litérature.

Dans ce projet ci, le choix de $f$ repose essentiellement sur ma curiosité suscitée par la lecture d’un papier sur l’EPF ou le TSF.

3. Workflow

L’application PowerExpect possède sa partie backend sur AWS et sa partie frontend sur Vercel. La contrainte que je me suis imposé sur ce projet est d’avoir une application qui se met à jour automatiquement tous les jours en suivant le rythme des enchères day ahead. Il fallait donc avoir une machine qui soit lancée tous les jours et exécute le code puis sauvegarde les résultats dans un lieu de stockage accessible via une API par le frontend. Le choix s’est porté sur AWS que je connaissais déjà. La pipeline CI/CD est assurée par CodePipeline et Codebuild qui récupèrent automatiquement le code dans mon répertoire github pour ensuite construire l’image Docker et la stocker dans ECR. Une instance EC2 est lancée tous les jours via une lambda controlée par EventBridge. L’instance va récupérer l’image dans ECR à son démarrage et l’exécuter. Tous les inputs mis à jour et les outputs sont sauvegardés dans deux buckets s3 distincts privés. Les logs sont également envoyés à mon adresse email par l’instance afin de ne pas avoir à se connecter à chaque fois à AWS ce qui est un peu pénible avec le MFA. Les fichiers sur s3 peuvent être volumineux et dépasser la limite du service d’amazon. J’ai donc opter pour le téléchargement directement sur s3 par le frontend via des URLs pré-signées d'1 seconde servies par une API.

4. Données

Le prix day ahead (ou SPOT) de chaque période de 15min du jour suivant est déterminé par une enchère pour chaque marché en Europe. Il y a donc 96 enchères pour la zone française et pour la zone allemande. Les participants ont jusqu’à 12h00 pour indiquer les volumes qu’ils veulent acheter/vendre en fonction du prix. Le prix pour chaque période t sera donc l’intersection entre les courbes agrégées de la demande à t et de l’offre à t de chaque participant [4].

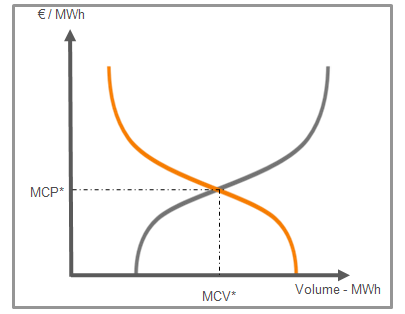
Les prix SPOT sont donc pilotés par l’offre (production) et la demande (consommation) qui sont eux mêmes pilotés par de nombreaux facteurs. La structure du marché en question, la composition du mix électrique, la météo, les marchés de réserve, les contraintes opérationnelles, la disponibilité des centrales, la saisonnalité/le calendrier (heure, jour, saison,…), les prix des combustibles et ceux du quota CO2 influencent l’offre. De même, la demande est influencée par des effets de saisonalité/calendrier et de température mais aussi par d’autres facteurs tels que les habitudes de consommation [5].

Les prix CAL+1, i.e. la série des prix des contrats calendaires échangés les bourses l’année Y pour livraison l’année Y+1 sont en cours d’ajout.

Comme toute série temporelle, les prix sont fortement corrélés aux valeurs précédentes. Une étude d’autocorrélation et de corrélation partielle sur les deux marchés permets de selectionner facilement des lags pertinents. J’ai chosisi des lags communs aux deux marchés pour simplifier les pipelines.

Pour l’instant, seuls les facteurs d’influence principaux et facilement disponibles comme la production et la demande totale sont utilisés afin de limiter la complexité des modèles. Fatalement, cela limite également leur capacité de prévision.

Les données proviennent essentiellement de la formidable plateforme de transparence ENTSOE . Ces données sont accessibles gratuitement via une API. Les modèles sont entrainés sur les données post-crise énergétique de 2022. L’horizon de prévision est pour l’instant d’une journée soit 96 points.

5. NHITS

a. Architecture

N-HiTS pour “Neural Hierarchical Interpolation for Time Series” [6] s’inscrit dans la catégorie des architectures DL à base de MLP qui ont maintenant prouvé être parmis les meilleurs options disponibles. Ce modèle a été introduit pour surmonter deux problèmes typiques de la prévision long terme: La complexité i.e. le coût en mémoire qui explose avec la taille de l’horizon, et la volatilité des prévisions i.e. la difficulté d’obtenir des prévisions fiables et stables à long terme.

Pour cela, les chercheurs sont parti du modèle NBEATS introduit 3 ans auparavant [7] pour ensuite l’améliorer en utilisant deux techniques: “L’échantillonnage de signal multi-taux” (Multi-rate Signal Sampling) et “l’interpolation hiérarchique” (Hierarchical Interpolation) [6].

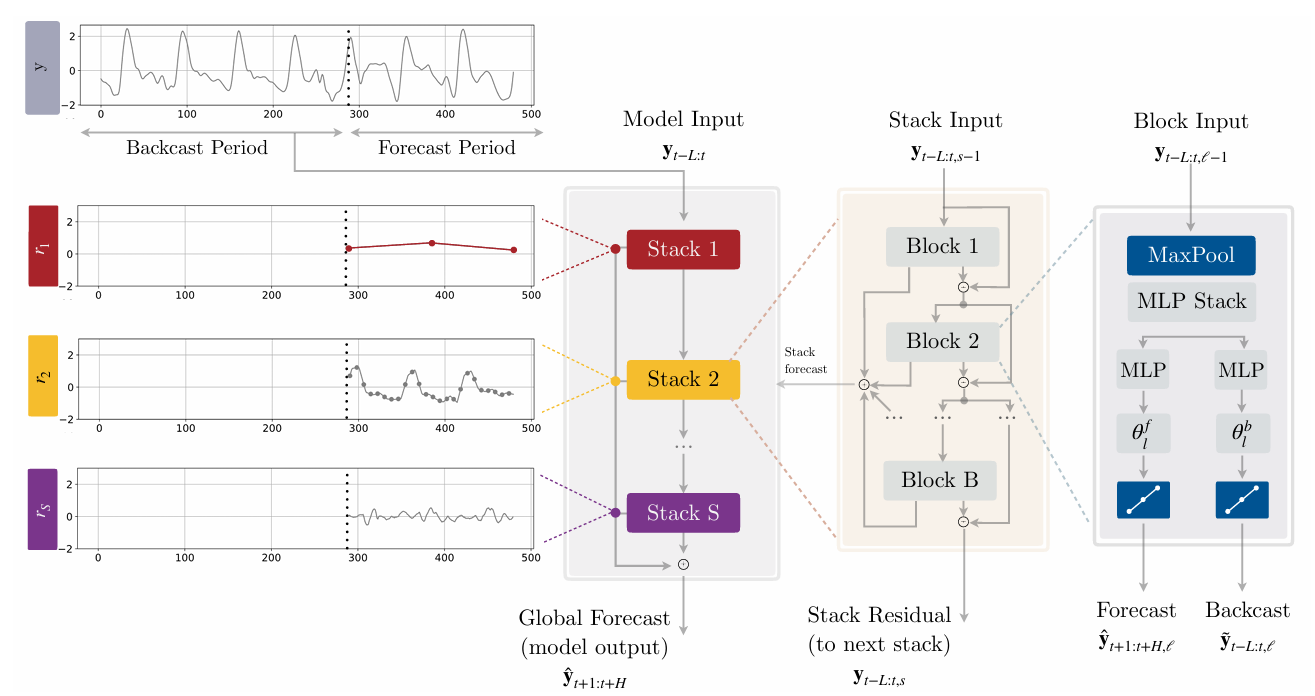
La figure ci-dessus illustre la version univariée de l’architecture de N-HiTS ce qui simplifie l’équation du problème posé en introduction mais qui est suffisante pour comprendre le fonctionnement du modèle (voir du côté de NBEATSx pour en savoir plus sur l’incorporation des variables exogènes à l’architecture [8]) Ainsi, cette version prend seulement en entrée le vecteur des observations passées noté ici $\pmb{y}_{t-L:t}$ avec $L$ le nombre de lags. On observe que N-HiTS repose sur une architecture à 3 “couches” avec S stacks composés chacun de B blocks. La couche de plus haut niveau correspond à la vue d’ensemble avec l’agencement des stacks, la suivante à l’agencement des blocks à l’intérieur de chaque stack et la dernière aux composants à l’intérieur de chaque block [6].

1ere couche

N-HiTS est composé de S stacks dont chaque stack va modéliser différentes fréquences de la série temporelle. Un stack s prend en entrée le résiduel du stack précédent $\pmb{y}_{t-L:t,s-1}$ (sauf pour le 1er stack bien sûr qui prend directement $\pmb{y}_{t-L:t}$ ) et retourne sa prévision $\pmb{\hat{y}}_{t+1:t+H,s}$ et son résiduel $\pmb{y}_{t-L:t,s}$ . Les prévisions de chaque stack sont additionnées pour former la prévision finale (le modèle renvoit également le résiduel du dernier stack S $\pmb{y}_{t-L:t,S}$ ) [6]:

\pmb{\hat{y}}_{t+1:t+H} = \sum_{s=1}^S \pmb{\hat{y}}_{t+1:t+H,s}

2ème couche

De manière similaire aux stacks (et comparable aux modèles de boosting), les B blocks d’un stack s sont assemblés hiérarchiquement où l’entrée du block $l$ est le résiduel du block $l-1$ . En effet, le backcast en sortie d’un block $l$ noté $\pmb{\tilde{y}}_{t-L:t,l}$ est utilisé pour nettoyer l’entrée $\pmb{y}_{t-L:t,l+1}$ du bloc suivant. Cela permet de concentrer l’attention des blocks sur des parties non comprises de la série. Les prévisions de chaque block sont additionnées pour former la prévision finale du stack. On a [6]:

\pmb{y}_{t-L:t,l+1} = \pmb{y}_{t-L:t,l} - \pmb{\tilde{y}}_{t-L:t,l}

\pmb{\hat{y}}_{t+1:t+H,s} = \sum_{l=1}^B \pmb{\hat{y}}_{t+1:t+H,l}

3ème couche

Chaque block commence par une couche de max pooling de taille de filtre $k_l$ suivie par un MLP. L’étape de pooling va permettre au block de se concentrer sur une fréquence spécifique de la série en entrée. Un grand $k_l$ filtrera les hautes fréquences forçant le MLP à modéliser une série à basse fréquence et réciproquement, un faible $k_l$ forcera le MLP à modéliser une série à haute fréquence. C’est ce qui est appelé “échantillonnage de signal multi-taux” ou “Multi-rate Signal Sampling”. Cette étape possède 2 avantages: Elle permet tout d’abord au modèle de se concentrer sur des aspects à large fréquence de la série temporelle ce qui permet de produire des prévisions à long terme plus stables et cohérentes, et ensuite, elle permet de réduire la taille de l’input en entrée du MLP, diminuant ainsi la compléxité du calcul (améliorant donc la vitesse d’entrainement) et le risque de surapprentissage. Avec $\pmb{y}_{t-L:t,l}$ le vecteur d’entrée du block $l$ , on a [6]:

\pmb{y}^{(p)}_{t-L:t,l} = MaxPool(\pmb{y}_{t-L:t,l}, k_l)

~

Le block $l$ va ensuite utiliser l’entrée réduite obtenue pour estimer les paramètres d’interpolation backward ${\theta}^b_l$ et forward ${\theta}^f_l$ en estimant avec un MLP le vecteur caché $h_b$ puis en le projetant linéairement [6]:

h_l = MLP_l(\pmb{y}^{(p)}_{t-L:t,l})

{\theta}^f_l = LINEAR^f(h_l)

{\theta}^b_l = LINEAR^b(h_l)

~

Enfin, les vecteurs de sortie du block $l$ $\pmb{\tilde{y}}_{t-L:t,l}$ et $\pmb{\hat{y}}_{t+1:t+H,l}$ sont obtenus par “interpolation hiérarchique” [6].

Une fois les coefficients ${\theta}^b_l$ et ${\theta}^f_l$ obtenus, il est necéssaire de rétablir le taux d’échantillonnage ou granularité initial(e) (modifié(e) par l’opération de max pooling / échantillonnage de signal multi-taux) afin de prévoir tous les points H dans l’horizon de prévision. Pour cela, N-HiTS effectue une “interpolation temporelle” via la fonction d’interpolation $g$ [6]:

\forall \tau \in \{t+1, \dots, t+H\}, ~\hat{y}_{\tau,l} = g(\tau,{\theta}^f_l)

\forall \tau \in \{t-L, \dots, t\}, ~\tilde{y}_{\tau,l} = g(\tau,{\theta}^b_l)

~

$g$ peut prendre la forme d’une fonction de plus proche voisin, linéaire par morceau ou cubique. Le papier indique qu’en moyenne sur l’ensemble des datasets testés, la précision des prévisions et les performances de calcul favorisent la méthode linéaire dont l’expression de $g$ est [6]:

g(\tau,\theta) = \theta [t_1] + (\frac{\theta [t_2] - \theta [t_1]}{t_2 - t_1}(\tau - t_1))

Avec:

$t_2 = t_1 + 1/r_l$
$t_1 = argmin_{t \in T:t\leq \tau} (\tau - t)$

La partition temporelle $T$ utilisée pour calculer $t_1$ est définie comme $T = \{t + 1, t + 1 + 1/r_l, \dots, t + H − 1/r_l, t + H\}$ où $r_l$ est appelé “ratio d’expressivité” et permet de contrôler le nombre de paramètres par unité de temps de sortie: $|\theta^f_l| = ⌈r_l H⌉$ (plus petit entier supérieur ou égal à $r_l H$ ). L’utilisation de ce ratio et de l’interpolation temporelle permet d’éviter l’explosion du coût en mémoire et de la complexité des calculs avec l’augmentation de l’horizon, problème récurrent dans les autres architectures comme les transformeurs.

N-HiTS va contraindre le ratio d’expressivité $r_l$ à se synchroniser avec la taille du filtre $k_l$ utilisé dans l’échantillonnage de signal multi-taux et c’est là que réside toute la puissance de l’architecture. En considérant une approche top-down (qui s’avère sur les datasets testés du papier plus efficace qu’une approche bottom-up), c-a-d. en choisissant des $r_l$ croissants et donc des $k_l$ décroissants, alors les blocks apprendront à la fois à observer et à générer des signaux avec une granularité/fréquence de plus en plus fine. Cette approche qui hiérarchise la spécialisation de chaque bloc et donc de chaque stack dans une fréquence précise est appelée “interpolation hiérarchique”. En choisissant de manière intelligente les $r_l$ , on peut faire correspondre la fréquence des blocks avec des cycles connus de la série temporelle comme les mois, semaines, jours,… [6]

En somme, N-HiTS est une généralisation de N-BEATS qui offre des prévisions précises, interprétables, stables sur tous les horizons, tout en minimisant son coût en mémoire et sa durée d’entrainement. N-HiTS vient fortement renforcer la puissance de la catégorie des architectures à base d’ensembles de MLP.

Avec le récent passage en octobre 2025 du pas horaire au pas 15min pour les marchés day ahead européens, multipliant ainsi l’horizon de prévision par 4, l’utilisation de modèles pensés pour la prévision long-terme comme N-HiTS est indubitablement devenue plus pertinente.

b. Hyperparamètres

Les hyperparamètres sont optimisés en utilisant l’approche par l’estimateur de Parzen à structure arborescente (TPE/Tree-structured Parzen Estimator) <a" href="#source-9">[9] implémentée dans hyperopt (voir section outils utilisés).

c. Entraînement

6. HSL

a. Architecture

Les modèles hybrides ou d’ensemble, qui combinent plusieurs modèles et méthodes sont un choix solide pour l’EPF/TSF [3]. Ils sont particulièrement efficaces pour saisir la dynamique complexe, non linéaire et volatile des marchés de l’électricité en tirant partie des forces de plusieurs architectures. Le papier qui présente le modèle suivant nous fournit un exemple de combinaison à utiliser spécifiquement pour l’EPF [10].

HSL pour “Hybrid Stacking Lasso” est un modèle hybride combinant 6 modèles de base: XGBoost, CatBoost, LightGBM, LSTM, GRU et NODE. Ces modèles de base sont combinés par stacking utilisant comme meta-modèle une régression linéaire Lasso [10].

Chaque modèle de base possède ses forces: XGBoost est robuste sur données structurées et possède une bonne capacité à capturer des interactions non-linéaires. LightGBM est efficace sur de gros jeux de données, ce qui permet un entraînement rapide et une bonne extraction de caractéristiques temporelles. CatBoost est performant dans son traitement des variables catégoriques et sa résistance au surapprentissage. LSTM et GRU sont inclus pour leur capacité à modéliser des motifs temporels à long terme. NODE, en combinant arbres de décision et réseaux de neurones, peut capturer des interactions complexes et non-linéaires sur données tabulaires [10].

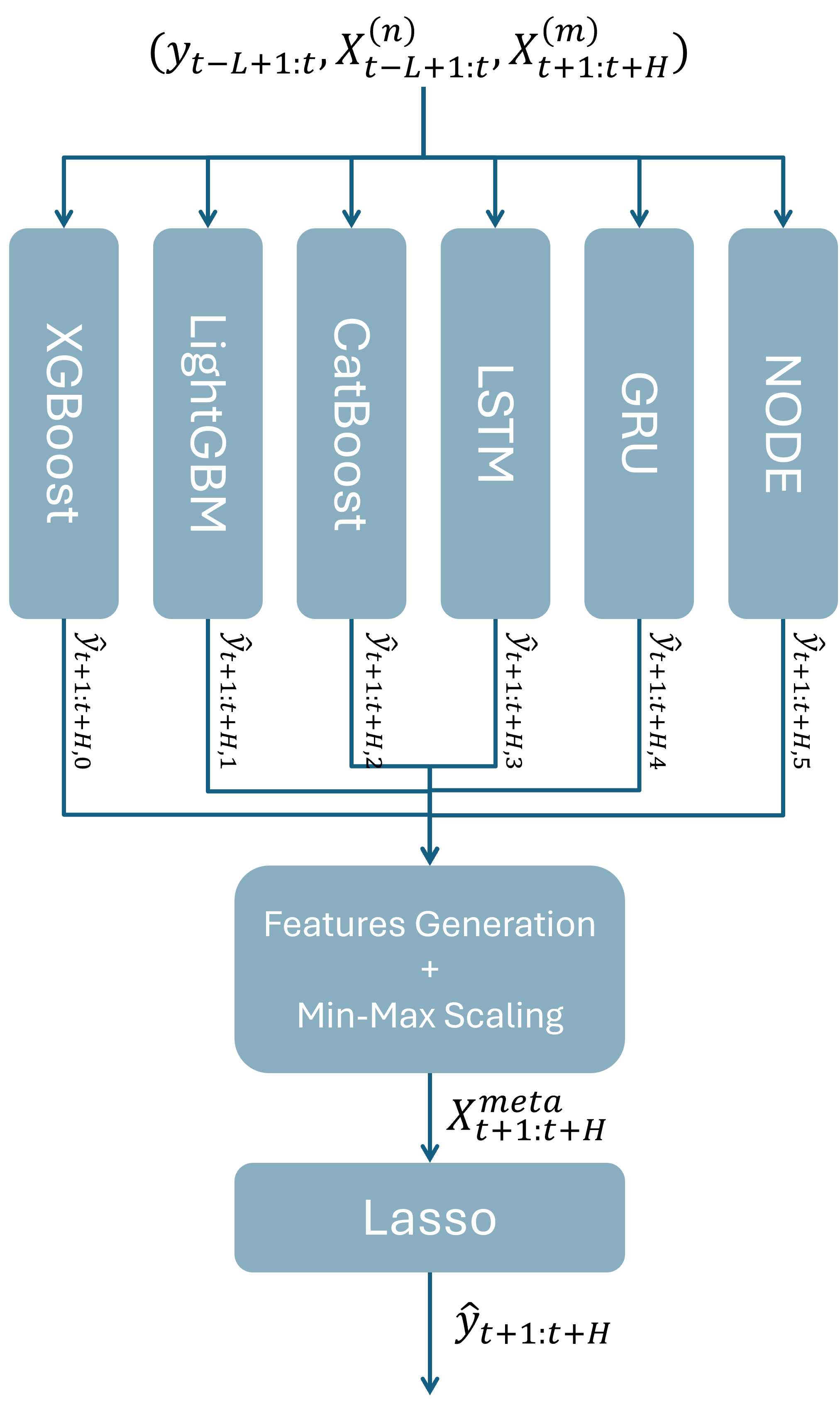
Les prévisions de chaque modèle de base sont concaténées puis normalisées sur $[0,1]$ par Min-Max:

\forall i \in \{0,\dots,5\}, ~\hat{y}^{scaled}_{t+1:t+H,i} = \frac{\hat{y}_{t+1:t+H,i} - min(\hat{y}_{t+1:t+H,i})}{max(\hat{y}_{t+1:t+H,i}) - min(\hat{y}_{t+1:t+H,i})}

$~$

Ensuite, la matrice regroupant les prévisions normalisées est augmentée avec des variables temporelles (heures, jours, semaines, etc…) pour constituer la matrice des meta-variables $X^{meta}_{t+1:t+H}$ utilisée en entrée du meta-modèle. L’article introduisant HSL ne donne pas d’informations sur les stratégies à mener pour entrainer le meta-modèle. On a donc ici le champs libre pour tester différentes choses tout en respectant la philosophie du papier original. J’ai alors suivi certaines recommandations du très bon article de Jason Brownlee sur les algorithmes de stacking [11]. Il indique par exemple qu’ajouter d’autres variables explicatives au meta-modèle peut lui fournir un contexte supplémentaire quant à la meilleure façon de combiner les prévisions issues des modèles de base. Des tests m’ont permis de confirmer cette approche. De plus, augmenter la taille de l’input n’est pas un soucis quand on utilise une régression Lasso comme meta-learner puisque les variables inutiles seront écartées. La prévision finale s’écrit:

\hat{y}_{t+1:t+H} = X^{meta}_{t+1:t+H}.W

~

Avec $W$ le vecteur de poids de dimension H. Ce vecteur est trouvé en minimisant la fonction objective $J$ sur la période d’entraînement $\tau$ où le terme de Lasso apparaît:

J(W) = L(y_{\tau}, \hat{y}_{\tau}) + \alpha||W||_1

Avec:

$L$ la fonction de perte (ici erreur moyenne absolue ou quadratique)
$\alpha$ le paramètre qui contrôle la force de la régularisation
$||W||_1 = \sum_i |w_i|$ La norme L1 (Lasso) appliquée aux poids du modèle

La régularisation Lasso/L1 met les poids à zéro dans les directions où la fonction de coût n’est pas sensible. Ainsi, lorsqu’on l’applique, on essaye de mettre à zéro les paramètres qui ne sont pas très importants ce qui permet de gérer de larges matrices d’input et de favoriser l’obtention d’une solution minimaliste. Regardons maintenant chaque modèle de base en détail.

b. XGBoost

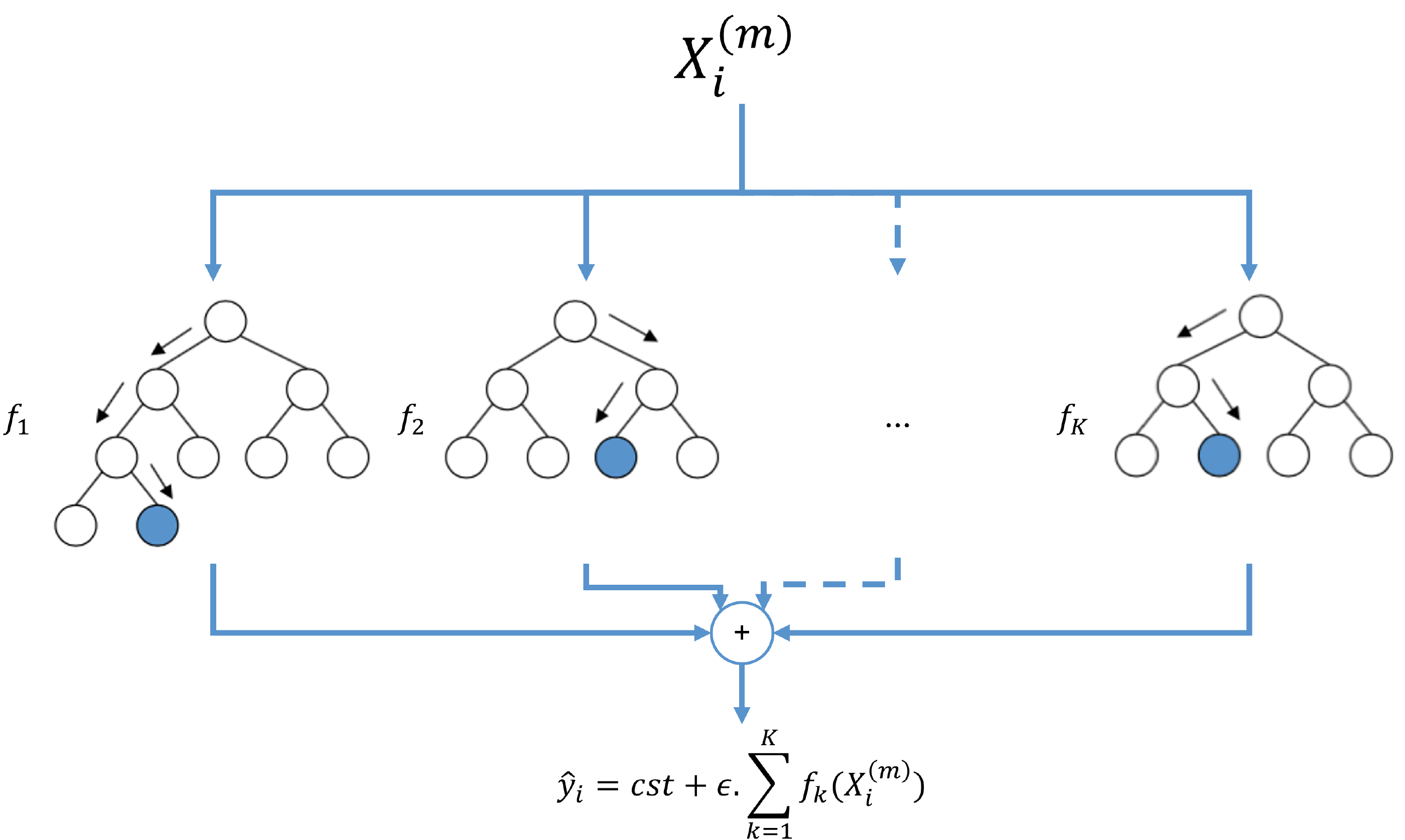
Architecture Gradient Boosting Machine/Tree

XGBoost pour “Extreme Gradient Boosting” est une architecture d’apprentissage automatique basée sur les GBM évoqués en introduction et développés au début du siècle. C’est un modèle d’ensemble qui utilise comme modèles de base des CART (“Classification And Regression Trees”) appelés “apprenants faibles”. Les CARTs sont similaires à des arbres de décision simples à la différence qu’un score est associé à chacune des feuilles leur permettant de traiter des problèmes de regression avec des variables continues.

Pour rappel, un arbre de décision est une méthode d’apprentissage supervisée non-paramétrique (= il n’y a pas d’hypothèses sous-jacentes sur la distribution des erreurs ou des données et le modèle est basé simplement sur les données observées). Il permettent de prévoir la valeur d’une variable cible en apprenant des règles de décision simples déduites des données observées. Ils sont très interprétables puisqu’ils illustrent directement et visuellement le processus de prise de décision. Cet interprétabilité s’estompe avec les méthodes d’ensemble.

XGBoost combine les arbres par boosting où la prévision du modèle correspond à la somme des prévisions de chaque arbre pour chaque pas de temps [12]:

\forall i \in \{t+1, \dots, t+H\}, ~\hat{y}_{i} = cst + \epsilon\sum^K_{k=1} f_k(X^{(m)}_{i})

Avec:

$K$ = le nombre d’arbres.
$f_k$ = la structure du k-ième arbre de regression.
$X^{(m)}_{i}$ = le vecteur des $m$ variables explicatives à l’instant $i$ .
$\epsilon$ = le taux d’apprentissage. Plus il est grand et plus les arbres vont devoir généraliser pour prévoir le résiduel empêchant ainsi le surapprentissage.
$cst$ = la prévision par défaut si le modèle ne contenait aucun arbre.

Les fontions $f_1$ à $f_K$ sont apprises par boosting en ajoutant un arbre après l’autre. D’où [12]:

\forall k \in \{1, \dots, K\}, \forall i \in \{1, \dots, n\},~\hat{y}^{(k)}_{i} = \hat{y}^{(k-1)}_{i} + \epsilon.f_k(X^{(m)}_{i})

~

Ainsi, le modèle va augmenter au fur et à mesure que des arbres sont ajoutés et chaque arbre va apprendre à prévoir le résiduel de l’arbre précédent. La fonction objective à minimiser pour entraîner le k-ième arbre va donc s’écrire [12]:

J^{(k)} = \sum_{i=1}^n l(y_i, \hat{y}^{(k)}_i) + \Omega (f_k) = \sum_{i=1}^n l(y_i, \hat{y}^{(k-1)}_i + \epsilon.f_k(X^{(m)}_{i})) + \Omega (f_k)

Avec:

$l$ la fonction de perte sur la i-ème observation.
$\Omega$ la fonction de régularisation.

Soit $w \in \mathbb{R}^T$ le vecteur des poids de chaque feuille $j \in \{1, \dots, T\}$ (avec $T$ = nombre de feuilles du k-ième arbre) et $q: \mathbb{R}^m \longrightarrow\ \{1, \dots, T\}$ la structure de l’arbre qui associe aux variables explicatives une feuille $j$ . On a : $f_k(X) = w_{q(X)}$ [12].

De plus, en considérant une régularisation ridge plus un terme $\gamma T$ pour encourager la construction d’arbres simples, on peut écrire:

\Omega (f_k) = \gamma T + \frac{1}{2} \lambda \sum^T_{j=1} w_j^2

~

$\lambda$ permet de réduire la sensibilité des poids $w_j$ aux valeurs observées et donc de limiter le surapprentissage.

Ainsi, en approximant $J^{(k)}$ par développement de Taylor d’ordre 2 et en simplifiant (= on supprime la somme des pertes qui est une constante et on pose $\epsilon = 1$ ), on obtient [12]:

\tilde{J}^{(k)} = \sum^T_{j=1} [w_j \sum_{i \in I_j} g_i^{(k)} + \frac{1}{2} (\sum_{i \in I_j} h_i^{(k)} + \lambda)w_j^2] + \gamma T

Avec:

$I_j = \{i | q(X^{(m)}_{i})=j \}$ l’ensemble des indices des $m$ variables explicatives associées à la j-ième feuille.
$g_i^{(k)} = \partial_{\hat{y}^{(k-1)}_i} l(y_i, \hat{y}^{(k-1)}_i)$ la i-ème dérivée partielle/gradient de premier ordre du k-ième arbre ou itération de boosting.
$h_i^{(k)} = \partial^2_{\hat{y}^{(k-1)}_i} l(y_i, \hat{y}^{(k-1)}_i)$ la i-ème dérivée partielle de second ordre du k-ième arbre ou itération de boosting.

Pour une structure $q$ donnée, le poids optimal de la j-ième feuille $w_j^*$ s’écrit alors [12]:

w_j^* = \frac{\sum_{i \in I_j} g_i^{(k)}}{\sum_{i \in I_j} h_i^{(k)} + \lambda}

Et la valeur optimale $\tilde{J}^{(k)^*}(q)$ :

\tilde{J}^{(k)^*}(q) = -\frac{1}{2}\sum^T_{j=1}\underbrace{\frac{(\sum_{i \in I_j} g_i^{(k)})^2}{\sum_{i \in I_j} h_i^{(k)} + \lambda}}_{cout~de~la~j~ieme~feuille} + \gamma T

Le coût $\tilde{J}^{(k)^*}(q)$ permet de mesurer la performance de la structure d’arbre $q$ en comparant le terme de régularisation sur le nombre de feuille au coût de chaque feuille. Plus $\tilde{J}^{(k)^*}(q)$ est petit, plus la structure de l’arbre est performante [12].

Si on utilisait la fonction erreur moyenne quadratique comme fonction de perte alors on aurait $g_i^{(k)} = \hat{y}^{(k-1)}_i - y_i$ et $h_i^{(k)} = 1$ . D’où:

w_j^* = \frac{\sum_{i \in I_j} (\hat{y}^{(k-1)}_i - y_i)}{|I_j| + \lambda} = \frac{somme~des~residuels~de~l'arbre~precedent}{nombre~de~residuels + \lambda}

et:

\tilde{J}^{(k)^*}(q) = -\frac{1}{2}\sum^T_{j=1}\underbrace{\frac{(\sum_{i \in I_j} (\hat{y}^{(k-1)}_i - y_i))^2}{|I_j| + \lambda}}_{cout~de~la~j~ieme~feuille} + \gamma T = -\frac{1}{2}\sum^T_{j=1}\frac{somme~au~carre~des~residuels~de~l'arbre~precedent}{nombre~de~residuels + \lambda} + \gamma T

~

Maintenant, il ne reste plus qu’à tester chaque structure possible i.e. chaque combinaison de split/division (= un noeud parent ou racine et deux feuilles enfants) possible et garder celle qui offre la meilleure performance (= plus petit $\tilde{J}^{(k)^*}(q)$ possible). Cette recherche est coûteuse en complexité et potentiellement aussi en mémoire puisqu’il faut calculer les coûts de chaque feuille possible et donc leurs gradients ( $o(T.m.(n-1))$ ).

La 1ère approche d’XGBoost est d’utiliser un algorithme exact (“Exact Greedy Algorithm”) qui va partir d’une feuille et ajouter les branches des meilleurs splits de manière itérative. Il parcourt toutes les valeurs triées des variables explicatives et cumule les gradients ce qui lui permet de diminuer le coût mémoire. Pour sélectionner le meilleur split, l’algorithme va choisir celui qui maximise le score suivant [12]:

score_{split} = \frac{1}{2}[cout~de~la~feuille~de~gauche + cout~de~la~feuille~de~droite - cout~de~la~racine] - \gamma

~

Plus le score est grand et plus le split fait baisser le coût de l’arbre.

Une fois la structure construite, XGBoost va l’optimiser en supprimant les splits qui ont un score négatif. Cet élaguage des arbres se contrôle avec le paramètre de régularisation $\gamma$ qui reflète ainsi une volonté plus ou moins grande d’avoir des arbres profonds i.e. une solution complexe susceptible de sur-apprendre [12]. D’autres paramètres permettent de gérer la complexité du modèle comme max_depth qui limite la profondeur maximale des arbres.

Généralement, XGBoost va utiliser des variantes de l’algorithme exact pour trouver les splits de manière plus optimisée. En effet, l’algorithme exact est coûteux en calcul et difficilement “scalable” puisqu’il teste tous les splits possibles. Par exemple, si les données d’entrée sont trop volumineuses, XGBoost va utiliser un algorithme (“Approximate Algorithm”) qui va réduire le nombre de splits testés à des centiles bien choisis [12].

En résumé, XGBoost va effectuer une prévision en sommant les prévisions de chaque arbre pour chaque pas de temps. Pendant l’entraînement, le modèle est construit en ajoutant un arbre après l’autre de manière cumulative. Chaque arbre est construit en commençant par une racine puis en ajoutant d’autres feuilles niveau par niveau. Les splits des feuilles sont choisis de manière à maximiser un score qui représente la contribution de la feuille à la réduction de l’erreur. XGBoost utilise différents termes de régularisation qui permettent d’éviter le surapprentissage et de limiter la complexité du modèle comme par exemple $\gamma$ qui est un seuil en dessous duquel on considère que le split contribue suffisamment à la réduction de l’erreur.

Comme XGBoost se base sur des arbres où des variables explicatives particulières sont choisies pour ses splits, on peut déduire le poids de chacune d’entre elles dans la prévision ce qui rend le modèle plus facilement interprétable que d’autres méthodes comme celles à base de réseaux de neurones. En plus de l’article fondateur [12], je conseille la série de vidéos de statquest pour plus de détails sur XGBoost.

c. LightGBM

LightGBM pour “Light Gradient Boosting Machine” propose comme XGBoost une implémentation optimisée d’un GBM (voir partie précédente). Cet algorithme pousse l’optimisation des performances plus loin qu’XGBoost en introduisant notamment 2 améliorations appelées “Gradient-based One-Side Sampling” (GOSS) et “Exclusive Feature Bundling” (EFB) [13].

Le défi des implémentations de GBM est toujours le même: comment optimiser la recherche des splits tout en préservant au maximum la performance ? L’approche naturelle est de réduire le nombre de splits candidats (en réduisant le nombre de splits à tester ou en résuisant la quantité de données observées) et de variables explicatives testées. LightGBM utilise l’algorithme GOSS qui conserve toutes les données qui présentent des gradients importants (suivant un seuil prédéfini) et effectue un échantillonnage aléatoire sur les données qui présentent des gradients faibles. En plus de GOSS, LightGBM introduit l’algorithme EFB qui va regrouper certaines variables explicatives entre-elles permettant ainsi de réduire l’espace de recherche des splits [13].

Une autre caractéristique importante de LightGBM est sa façon de construite ses arbres. Contrairement à d’autres implémentations comme XGBoost qui le font niveau après niveau, LightGBM va constuire ses arbres feuilles après feuilles en choisissant (selon un critère) la meilleure feuille suivante à traiter. A nombre de feuilles égal, cette approche à tendance à obtenir de meilleurs résultats. Voir la documentation de la librarie (section outils utilisés) pour plus d’informations sur ce sujet [13].

d. CatBoost

CatBoost pour “Categorical Boosting” est comme XGBoost et LightGBM une implémentation d’un GBM (voir section XGBoost pour les notations). CatBoost se distingue par son traitement des variables catégoriques et son approche du boosting pour résoudre des problèmes de fuite de la variable cible [14].

Variables catégoriques

Une variable explicative catégorique est composée d’un ensemble discret de valeurs distinctes appelées catégories. Par exemple en prévision de séries temporelles, on considère parfois des moments de la journée (matinée, après-midi, soirée,…). Ces variables catégoriques peuvent apporter un gain substentiel d’information. Cependant, elles nécessitent une étape cruciale d’encodage, i.e. de transformation des catégories en valeurs numériques compréhensibles par le modèle et avec un minimum de perte d’information [14].

Il existe plusieurs méthodes d’encodage de variables catégoriques . Une méthode classique d’encodage est le “one-hot encoding” qui consiste à convertir chaque catégorie en vecteur colonne binaire (1 pour les indices où la catégorie apparait et 0 sinon). Evidemment, cette méthode est vite limitée par le nombre de catégories à encoder. Une autre méthode populaire est le “target encoding” qui consiste à remplacer les catégories par des valeurs statistiques de la variable cible. On peut par exemple utiliser la moyenne des valeurs de la variable cible sur chaque catégorie. Cette approche brute est à proscrire puisque qu’elle va déboucher sur une fuite des données. En effet, les données de test vont contenir des informations des données d’entrainement. Plusieurs méthodes sont possibles pour résoudre ce problème comme la partition des données d’entrainement [14].

CatBoost utilise une stratégie de “target encoding” décrite comme plus effective par le papier fondateur. De manière simple, CatBoost va encoder les catégories basées uniquement sur les valeurs observées précédentes. Cela veut dire que CatBoost va traiter séquentiellement l’encodage des catégories évitant ainsi toute fuite de la cible. Comme l’ordre des catégories a une importance, cette approche est appelée “encodage ordonné de la cible” (“ordered target statistics” ou “ordered target encoding”). La valeur numérique de la catégorie va être alors calculée comme la moyenne des observations passées pour cette catégorie lissée d’une constante (“prior”) $p$ telle que la valeur de la catégorie $k$ à l’indice $i$ s’écrit [14]:

x_i^k=\frac{\sum_{j\in I_i^k}y_j + p}{|I_i^k| + 1}

~

Avec $I_i^k$ l’ensemble des indices précédant l’indice $i$ où $y$ vaut 1 pour la catégorie $k$ (lorsque la cible est continue, on utilise simplement des intervalles statistiques/“bins”).

Lors de l’inférence, les catégories sont encodées en reprenant toutes les valeurs encodées précédemment [14].

Boosting ordonné

Tout comme l’encodage ordonné pour le traitement des variables catégoriques, le boosting ordonné est motivé par la présence d’une fuite de la cible pendant l’entraînement. En effet, les auteurs du manuscrit original de CatBoost montrent que sur un exemple simple où l’on utilise le même ensemble de données pour entraîner chaque arbre, un biais inversement proportionnel à la taille de l’ensemble de données va décaler la prévision. Cela provient de l’utilisation des mêmes variables cibles pour l’estimation des gradients et l’entrainement des arbres. En effet, on calcule les $g_i^{(k)}$ en utilisant la cible $y_i$ et la prévision $f_{k-1}(x_i,y_i)$ alors que l’arbre $f_{k-1}$ a été lui même construit en utilisant $y_i$ . C’est une fuite de la cible qui cause un décalage de la distribution conditionnelle des gradients $g_i^{(k)}(x_i,y_i)|x_i$ (et donc de $f_k(x_i,y_i)|x_i$ ) par rapport à celle sur les données de test et in fine débouche sur une prévision biaisée et un modèle qui généralise moins bien. Pour y remédier, CatBoost utilise le “boosting ordonné” [14].

Le boosting ordonné propose de résoudre le problème de fuite en utilisant les exemples précédents $(x_{0:i-1},y_{0:i-1})$ pour entraîner $f_{k-1}$ . Ainsi, $f_{k-1}(x_i,y_i)$ n’a jamais vu l’exemple $(x_i,y_i)$ et les $g_i^{(k)}$ ne seront pas estimés avec un $f_{k-1}$ biaisé. Cette approche est la même que celle utilisée pour l’encodage ordonné des variables catégoriques en traitant séquentiellement, ligne par ligne, les données [14].

L’implémentation naive ou brute force du boosting ordonné consisterait à entraîner n (=nombre d’exemples/observations, $i \in \{1, \dots, n\}$ ) modèles $M_1, \dots, M_n$ , tels que le modèle $M_i$ est entraîné uniquement sur les i èmes observations d’une permutation aléatoire du jeu de donnée. Ensuite, on utilise le modèle $M_{i-1}$ pour calculer $g_i$ . Toutefois, cette solution naïve est trop complexe: entraîner n modèles aurait un coût trop grand en temps et en mémoire. Pour réduire la compléxité de l’implémentation et utiliser le boosting ordonné, CatBoost va procéder de la manière suivante [14].

Tout d’abord, CatBoost génère un ensemble de permutations aléatoires de l’ensemble des données, sur lesquelles effectuer l’encodage ordonné puis entraîner chaque arbre. Ainsi, les gradients $g_i^{(k)}$ et les variables catégoriques seront calculés en utilisant un historique différent à chaque étape de boosting $k$ . Cela garantit toujours qu’aucun modèle n’a vu l’exemple pour lequel on calcule le gradient, mais diminue l’instabilité due au fait qu’un exemple en début de permutation aurait très peu de données antérieures [14].

Ensuite, CatBoost entraîne ses apprenants faibles qui sont des arbres de décision symétriques ou “inconscients”, i.e. des arbres dont toutes les feuilles d’un niveau possèdent le même split/critère de division. Ces arbres sont moins sujets au sur-apprentissage et permettent d’accélérer considérablement l’exécution au moment des tests. Les arbres sont appris de manière séquentielle où le gradient $g_i$ est calculé en utilisant la prévision $M_{r,j}(i)$ du i-ème exemple en utilisant les j-ièmes premiers exemples de la permutation r. En pratique, au lieu de conserver toutes les prévisions $M_{r,j}(i)$ , CatBoost ne conserve que des prévisions intermédiaires à intervalles géométriques (aux indices $2^k$ ). Cela est possible grâce à la structure symétrique des arbres. Ainsi, si on a s permutations, alors la complexité pour mettre à jour les modèles $M_{r,j}$ et calculer les gradients passe de $O(sn^2)$ à $O(sn)$ [14].